There’s a common piece of advice when people learn to read typing rules: “read them clockwise”. I’m going to explain how to generalise this idea into a useful concept called a mode, but first let’s explain the advice itself!
(As a quick aside, I have some slight quirks in how I write variables in typing rules - this post explains what I do differently and why)
Reading Clockwise
Suppose I want to use this rule:
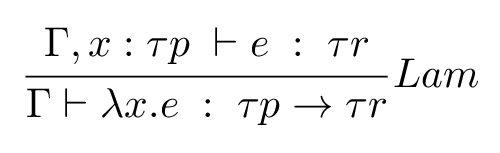
We can break it down into steps, reading the rule clockwise starting from the bottom-left.
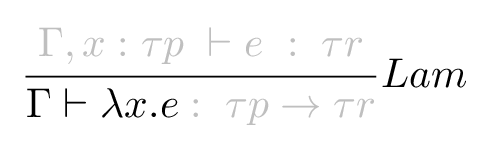
This rule assumes we have some context Γ and we want to typecheck λx.e, a lambda with some variable x and the body e. Notice that we’ve taken not even a syntactic but a lexical slice out of the rule - Γ ⊢ e : τ is all one judgment/relation, so Γ ⊢ e on its own doesn’t really mean anything. It’s the variables Γ and e that matter.
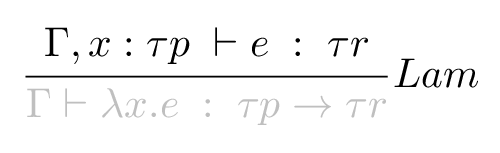
To continue, we have to check the conditions above the line hold. In this case, that we can typecheck e in the context Γ, x : τp where we have no idea what type τp is yet but we call the resulting type τr
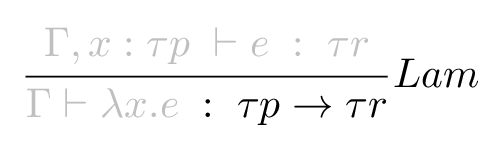
Finally we get our result type, τp → τr - and hopefully we found out what τp is on the way.
Clockwise is a Mode?
The “clockwise” rule of thumb relies on a simple trick: typechecking is the process of starting with some term (and some assumed context) and figuring out what valid type it has. Slightly informally, if we’re doing type synthesis/inference we don’t know that type yet and if we’re doing type checking then maybe we do, but that part’s less important for a moment.
Usefully, when we make a recursive check like in the Lam rule, we have the same situation again - the same parts of the typing relation are input, the same parts are output.
And because most type systems are syntax-directed1, we can find the rule we need just by looking at the term - letting us write a recursive type checker by simple case analysis.
Modes
“Clockwise” the way I’ve just described it, complete with that commonality in uses above and below the line? It’s something called a “mode” 2, and I might write that mode down + ⊢ + : −. Here, + is a known parameter and − is an unknown we’re trying to find out. That doesn’t mean there can’t be any unknowns buried in something +, we don’t know what τp is when we typecheck that lambda body. But we do know that it’s the τp we introduced in that rule and not an “unknown unknown”!
But there are other modes we can use that Lam rule in, so let’s talk about them a bit? Here are some examples:
| Mode | Use |
|---|---|
| + ⊢ + : + | Type checking |
| + ⊢ + : − | Type synthesis |
| − ⊢ + : + | Free variable analysis (checked type) |
| − ⊢ + : − | Free variable analysis (synthesised type) |
| + ⊢ − : + | Proof search |
| Program synthesis |
All of these things can be done with the same rules! As an old logic programming slogan says: “algorithm = logic + control”. Modes declare an important piece of control information without forcing us to detail things with step-by-step instructions.
Another important related concept from logic programming is the relationship between relations and procedures. Typing rules describe [part of] a relation, procedures implement specific ways of using a relation - and different modes often need different procedures to run efficiently.
As we’re talking about type systems in particular, I should also spell out clearly: bidirectional type systems work by limiting which rules can be used at which modes (“checking”, “synthesis”)!
Many Notions of Mode
There are many flavours of mode system out there - not least because logic programming has a wide and varied history! Something that is suitable for Prolog might be unsuitable for studying formal logics, because in Prolog a lot comes down to variable instantiation. Something suitable for studying formal logics is likely to be utterly unsuitable for Prolog: it’s turing complete and permits all kinds of things that formal logics normally avoid to have a tractable metatheory.
One extension I’ve found useful is one I call “refinement modes”, by analogy to refinement types. It comes from what you might call the “variable instantiation” side of the family and allows the mode for a particular variable to be “input, and it’s definitely a → but I don’t know the parameters”, or “output, and it’s a →…”. The Mercury language supports something like this, and I’ve used it in my own work.
Another important concept is ground mode - the mode in which everything is fully known and there are no (meta)variables in the data at all. Something at ground mode doesn’t need any hint of constraint solving, not even first-order unification! This is why it’s so much faster to write a typechecker for simply typed lambda calculus with annotated lambdas than to allow leaving off the type annotations.
Ground mode is also a link between functional and logic programming: functional programming normally works at ground mode. Given the Curry-Howard correspondance, arguably functional programming is 0th order logic programming!
Ack
Hopefully this has been some help to somebody out there! I’d like to thank a couple of people:
- Chris Martens is from a more logic-oriented background than I am, and I’d especially like to thank them for pointing me towards a useful citation trail for my MSFP2020 submission! After a short chase I ended up using these two papers:
- More importantly for this piece, Uma Zalakain let me know a slide or two about modes in my work made a big difference for how she thinks about type systems. It’s easy to lose track of what other people do and don’t know, both as fields expand and as we get older, stop being students and start forgetting where we even learned things. This post is an attempt to make something useful common knowledge, and without Uma’s feedback I wouldn’t have written it.
Each rule covers specific pieces of syntax and each piece of syntax has one rule↩︎
Conor McBride rearranges the rules so that regardless of the mode, information always flows clockwise and we never find new information going counterclockwise. In his systems, clockwise is the direction time flows in.↩︎